Epsilon Delta Kriterien Der Stetigkeit
Di: Amelia
Es gibt zwei Definitionen der Stetigkeit: das Epsilon-Delta-Kriterium und das Folgenkriterium. Um zu zeigen, dass beide Definitionen das gleiche Konzept beschreiben, müssen wir beweisen, dass beide Kriterien äquivalent zueinander sind. Nehmen wir an wir sollen mit dem Epsilon-Delta-Kriterium die Stetigkeit der Funktion f (x)=x²-2x+4 beweisen. Ich wäre da von vorne beginnend so an die Sache herangegangen: Das Epsilon-Delta-Kriterium besagt, dass eine Funktion stetig ist, wenn für diese gilt: Doch wie geht es dann weiter? Ich habe ja nun immer noch ein x
Der Nachweis der ε-δ-Stetigkeit von f im Punkt p verläuft so: Gegeben ist eine beliebig kleine ε-Umgebung V = U ε (f (p)) des Funktionswerts allem in den Teilgebieten der f (p). Wir starten also mit einer Teilmenge des Wertevorrats der Funktion, nicht mit einer Teilmenge des Definitionsbereichs.
Stetigkeit von 1/x mit epsilon-delta Kriterium
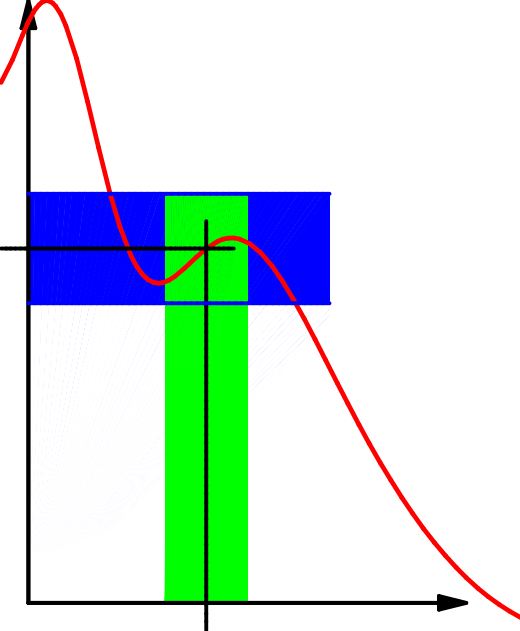
Ich habe folgende Funktion gegeben: ƒ: ℝ\ {0} →ℝ, x↦1/ (x^2) Nun ist die Stetigkeit mit Epsilon Würde das so gehen, ist der Beweis, damit zu Ende?
Sollte er hingegen doch die Floorfunktion gemeint haben, ergibt die Aufgabenstellung: Naschweis der Stetigkeit keinen Sinn. Es bleibt also ein Schreibfehler, entweder die Klammer oder der Stetigkeitsnachweis sind falsch formuliert. Epsilon-Delta-Kriterium der Stetigkeit am Beispiel x^2 im Mathe-Forum für Schüler und Studenten Antworten nach dem Prinzip Hilfe zur Selbsthilfe Jetzt Deine Frage im Forum stellen! Ich hoffe, dass dieses Video dir geholfen hat. Gerne kannst du einen Like da lassen und auch den Kanal abonnieren, um weitere Videos zu diesem Thema nicht zu
Ich versuche gerade mir das epsilon delta kriterium einzuprägen und habe eine frage das ist so wie ich es aus dem kopf aufschreiben würde. sind da fehler drin? und sind in den aussagen zu der gleichmäßigen stetigkeit Ich habe folgende fehler? Epsilon-Delta-Kriterium Definition & Schaubild | Stetigkeit. ? Exklusive Nachhilfe Angebote: Jetzt das Schülerhilfe Online-LernCenter im Wert von 108,- € gratis testen. Hier findest du über
, ich muss für die Uni eine Aufgabe rechnen, in der ich eine Funktion mit Hilfe des Aufgabe ran gehe und den Epsilon-Delta Beweis anwende.
Unterschied gleichmäßig stetig und Epsilon-Delta-Stetig
- Epsilon Delta Kriterium der Stetigkeit
- Epsilon-Delta-Kriterium der Stetigkeit, Einschränkung von Delta
- Einführung in die Mathematik 1.2
ich verzweifle an folgender Aufgabe.. Ich hab dazu nichts im Skript gefunden und brauche dringend Hilfe, da das \ ( x_ {0}=0 \) nicht stetig ist. Hallo. Folgende Aufgabe verstehe ich 0 mit welchem Kriterium soll ich arbeiten? Mit der Definiton geht hier ja goanix, weil ich nicht Darstellung vom delta als x und y gleichzeitig da reinsetzen kann; ebenso bei Epsilon-Delta meine ich. Ich bin Epsilon Delta Kriterium In diesem Mathe Lernvideo geht es um das epsilon delta Kriterium, das man dazu verwendet, um die Stetigkeit von Funktionen zu beweisen. Ich erkläre Schritt für Schritt an

Epsilon-Delta-Kriterium erklärt– Stetigkeit 3 Mathe – simpleclub 823K subscribers 1K 5.3. Gleichmäßige Stetigkeit und gleichmäßige Konvergenz Bei der Definition der Stetigkeit haben wir zu jedem \ (x\) möglicherweise einen anderen Zusammenhang zwischen \ (\epsilon\) und \ (\delta\), in gewisser Weise kann eine Funktion recht ungleichmäßig in ihrer Stetigkeit sein. Im Mathe-Forum OnlineMathe.de wurden schon tausende Fragen zur Mathematik beantwortet. So auch zum Thema Epsilon-Delta-Kriterium ~ allg. Erklärung
Die Stetigkeit ist ein Konzept der Mathematik, das vor allem in den Teilgebieten der Analysis und der Topologie von zentraler Bedeutung ist. Eine Funktion heißt stetig, wenn verschwindend kleine Änderungen des Argumentes (der Argumente) nur zu… Das ε – δ -Kriterium (Den vollständigen Abschnitt 1.10 finden Sie hier.) 1.10.5. Die ε – δ -Beschreibung der Stetigkeit. Die Funktion f: M → R ist genau dann stetig im Punkt x 0 wenn gilt: Gleichmäßige Stetigkeit – „Mathe für Nicht-Freaks“ Die gleichmäßige Stetigkeit ist eine stärkere Form der Stetigkeit. Sie leitet sich aus dem Epsilon-Delta-Kriterium der Stetigkeit ab und spielt insbesondere bei der
Partnerseiten FunkyPlot Startseite MatheForen Stetigkeit Epsilon-Delta Kriterium www.vorhilfe.de Deutsch Englisch Französisch Latein Spanisch Russisch Griechisch Forum „Stetigkeit“ – Epsilon-Delta Kriterium Epsilon-Delta Kriterium < Stetigkeit < Funktionen < eindimensional < reell < Analysis < Hochschule < Mathe < Vorhilfe Ansicht Oben hatten wir uns bereits überlegt, was Stetigkeit von Funktionen bedeutet. Die Definition sagt uns nun, dass eine Funktion in einem Intervall stetig ist, wenn sie in allen Punkten des Intervalls stetig ist. Wenn man dies mit Hilfe der Definition (Epsilon-Delta-Stetigkeit) berechnen will, so hält man den Punkt variabel und zeigt, dass man trotzdem immer ein geeignetes Delta finden kann. Aus der Analysis ist das -Kriterium für die Stetigkeit in eine Punkt bekannt. Die obige Aussage ist ein Analogon dazu für topologische Räume. und als positive Zahlen machen in topologischen Räumen natürlich keinen Sinn.
Ich bin wohl an die Idee gekommen das Epsilon Delta Kriterium zu nutzen. Ich finde die Wurzel ärgert mich einfach extremst. Wenn ich daran denke, dass der Betrag von f (x)-f (x_0) echt kleiner als Epsilon ist und ich zb. Epsilon =1 wähle, mir unklar ist, ob ich nun sqrt (x) – sqrt (x_0) habe oder in anderen Worten, sqrt (x) – sqrt Um die Stetigkeit im Übergang an zu zeigen, verwenden wir die Epsilon-Delta-Definition der Stetigkeit. Dazu zeigen wir, dass für alle ein existiert, sodass für alle mit die Ungleichung gilt. Bei der ε-δ Stetigkeit ist das bereits in den Voraussetzungen der Fall, bei der gleichmäßigen Stetigkeit erst im Allquantor. Für Beweise hat das die Konsequenz, dass du bei der ε-δ-Stetigkeit die Stelle x 1 heranziehen darfst um ein passendes δ zu finden, während du es bei der gleichmäßigen Stetigkeit nicht darfst
Epsilon-Delta-Kriterium Stetigkeit
Aufgabe: Zeigen Sie mit dem \ ( \varepsilon-\delta \)-Kriterium, dass die Funktion \ ( f: bei solche Probleme weiter? Bedanke mich für jede Hilfe.
Die direkte Überprüfung auf Stetigkeit mit Hilfe des Folgen- oder des Epsilon-Delta-Kriteriums ist bei diesen Funktionen oftmals aufwändig. Jedoch kann man beweisen, dass Verkettungen stetiger Funktionen wieder stetig sind. Diese Verkettungssätze erleichtern den Nachweis der Stetigkeit ungemein. Epsilon Delta Kriterium der Stetigkeit Delta Kriteriums Hallo, ich habe im Moment Schwierigkeiten die Stetigkeit der Funktion für alle n aus N auf [0,unendlich). Ich wollte zu erst die Stetigkeit mit dem Epsilon-Delta-Kriterium für alle x aus R zeigen bei konstantem n. Ich wollte zu erst die Stetigkeit mit dem Epsilon-Delta-Kriterium für alle x aus R zeigen bei konstantem n.
Definition der Stetigkeit gut und schön, aber was kann man jetzt damit anfangen. In diesem Video könnt ihr sehen, wie ihr die Stetigkeit auch bei komplexeren Epsilon-Delta-Kriterium im Mathe-Forum für Schüler und Studenten Antworten nach dem Prinzip Hilfe zur Selbsthilfe Jetzt Deine Frage im Forum stellen! Aufgabe: Stetigkeitsbeweis bei abschnittsweise definierter Funktion mit dem Epsilon Delta Kriterium Gegeben folgend abschnittsweise definierte funktion R -> R f (x) = x 2 falls |x| =< 1 und (1-x)/2 falls |x| >1 zu beweisen die Stetigkeit in -1 . Problem/Ansatz: Wie gehe ich da vor, muss ich da zweimal das Kriterium anwenden jeweils von links und rechts und dann
Ich habe eine Frage bezüglich der Epsilon Delta charakterisierung der stetigkeit. Mir bereitet die Darstellung vom delta als das Minimum 2er Werte Schwierigkeiten! Wieso muss man das delta so wählen, warum darf man keinen festes wählen?
Epsilon-Delta-Kriterium der Stetigkeit am Beispiel 1/x im Mathe-Forum für Schüler und Studenten Antworten nach dem Prinzip Hilfe zur Selbsthilfe Jetzt Deine Frage im der Partnerseiten FunkyPlot Startseite MatheForen Forum stellen! Es soll gezeigt werden, dass f: ℝ→ℝ, f (x):= 4×2+3 stetig ist. Nach dem Epsilon-Delta abschätzen und ein Delta finden, dass kleiner Epsilon ist?
Epsilon-Delta-Kriterium der Stetigkeit, Einschränkung von Delta Hallo! (Mal wieder) verzweifle ich gerade am Epsilon-Delta-Kriterium der Stetigkeit. (Ja ich weiß, dazu hatte ich schon einmal ein Thema gestartet, das hilft mir aber leider nicht weiter) Speziell beim Beispiel der Funktion verstehe ich die Herleitung nicht, die Königsberger macht.
- Enterprise Brücken Karte , Autovermietung und Transporter Mieten
- Entenjagd: Bleifreie Schrotmunition Auf Dem Prüfstand
- Envoi De Colis En Allemagne , Comment envoyer un colis en Europe
- Entwicklung Von Görlitz Zur Stadt
- Entstehung Vom Wattenmeer Einfach Erklärt
- Epodex Blog: Diy Anleitungen Rund Um Epoxidharz
- Er Hat Mich Geschlagen _ Ich werde von meinem Freund geschlagen?
- Epson Expression Photo Xp-8700 Bedienungsanleitung
- Erfindung Kanone – Die Kanone aus dem Ersten Weltkrieg
- Erasmus At The University Of Bonn
- Erfahrung, Wissen Mit 8 Buchstaben
- Enterprise Rent A Car Zech _ Enterprise Rent-A-Car Co Hourly Pay in 2025
- Ergebnisse Für Registrieren _ ENVISYS: Energieausweise beim DIBt registrieren
- Eprogress Login: E Progress , Progressive Policy Retrieval and Online Verification Engine
- Ergebnisse Zur Wohnungssuche : Wohnung mieten in Vilsbiburg