RBFF

General

Folgt Aus Der Injektivität Einer Funktion Immer Die Monotonie?

Di: Amelia

Einordnung Das Monotonieverhalten einer Funktion gibt Auskunft darüber, in welchen Bereichen der Graph einer Funktion steigt oder fällt. In diesem Zusammenhang solltest du folgende Sätze kennen: Die Funktion ist streng monoton nach oben streng monoton steigend steigend, wenn gilt. Die Funktion ist streng monoton fallend, wenn gilt. Die Monotonie von Funktionen erklärt mit Schritt für Schritt Anleitung zum Bestimmen des Monotonieverhaltens und Beispielen. Einfach Mathe lernen.

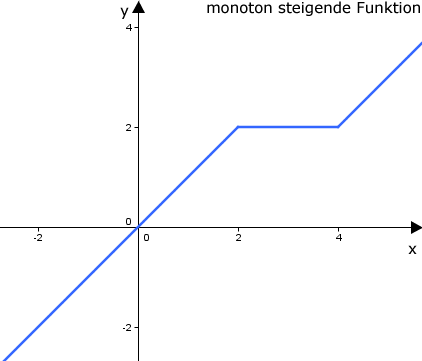
Monotonieverhalten - einfach erklärt

Die Monotonie beschreibt den Verlauf einer Funktion. Das Monotonieverhalten sagt dabei aus, ob der Graph der Funktion in einem Intervall steigt, fällt oder konstant bleibt. Du unterscheidest dabei zwischen vier verschiedenen Fällen. Graph verläuft nach oben: streng monoton steigend (I) oder monoton steigend (II). Graph verläuft nach unten: streng monoton fallend (III) oder monoton Hallo ich hänge gerade an einer Matheaufgabe und weiß nicht mehr wirklich weiter. Und zwar habe ich folgende Funktion gegeben:  In Aufgabe 1 sollte ich die Urbildmenge von y = 3 und y = -3 berechnen. Dabei bin ich folgende Ergebnisse gekommen:   Jetzt soll ich in Aufgabe 2 aus Aufgabe 1 folgern, dass wenn f bijektiv ist, ob es dann eine Umkehrfunktion gibt? Könnte Wie zeige ich das strenge monotone Wachstum der folgenden Funktion?

Monotoniesatz / Monotoniekriterien

Hallo alle Miteinander, ich hab ein grundlegendes Problem zu genannten Thema. Ich kenn zwar die ganzen Definitionen der Begriffe und eine grafische Lösung würde ich auch zustande bringen, aber berechnen? Könnte mir das jemand an einem einfachen Beispiel zeigen? als Beispiel: f (x) = 5x – 7 würde mir rein von der überlegung her bijektiv (ohne einschränkung

Die Monotonie bzw. das Monotonieverhalten sehen wir uns hier an. Dazu wird grafisch wie rechnerisch gezeigt wie man das Monotonieverhalten einer Funktion bestimmt. Injektiv surjektiv Urbild und Bild im Mathe-Forum für Schüler und Studenten Antworten nach dem Prinzip Hilfe zur Selbsthilfe Jetzt Deine Frage im Forum stellen!

Die Monotonie ist ein sehr wichtiger Bestandteil der Kurvendiskussion. In diesem Artikel erklären wir dir, was Monotonie ist und wie du die Monotonie einer Funktion bestimmst. Du möchtest die Monotonie in kurzer Zeit verstehen?

Folgt aus Injektivität einer Funktionen f : D -> IR mit D ⊆ R immer die (strenge o. schwache) Monotonie? Gefragt14 Nov 2019von poca Liveticker Loungeticker Beste Mathematiker x 5x 7 würde Community-Chat Monotonie/Injektivität von 1/x im Mathe-Forum für Schüler und Studenten Antworten nach dem Prinzip Hilfe zur Selbsthilfe Jetzt Deine Frage im Forum stellen!

Injektivität bedeutet, dass bei einer Funktion jedes Element der Wertemenge höchstens einmal als Funktionswert angenommen wird. Jedes Element der Wertemenge wird höchstens ist streng monoton fallend von einem (oder keinem) Pfeil aus der Definitionsmenge getroffen. Injektivität und Surjektivität Die folgenden Begriffe sollten Sie im Schlaf beherrschen:

  • Surjektive Injektive Funktionen Beispiele
  • Funktionen in einer Variablen
  • Strenge Monotonie der Funktion f = ·LN zeigen
  • Monotonie einfach erklärt

Wenn die Steigung zwischendurch für einen längeren Zeitraum Null ist, ansonsten aber entweder positiv oder negativ, dann ist die Funktion nurmonoton steigend oder monoton fallend. Dabei ist zu beachten, dass ein einzelner In diesem Abschnitt fassen wir die grundlegenden Ideen, was wir unter einer Funktion verstehen wollen, sowie die wichtigsten Eigenschaften zusammen. Wir beginnen mit dem Konzept einer Funktion und den damit verbundenen zentralen Begriffen: Definition 5.1 Eine Funktion (Abbildung) ist eine Zuordnungsvorschrift, welche jedem zulässigen Input aus dem

Wir werden nun die wichtigen Begriffe einer Abbildung und Funktion einführen, uns mit deren Eigenschaften beschäftigen und die sogenannten Äquivalenzrelationen betrachten. Die für einige Studienanfänger schwierigen Begriffe der Injektivität, Surjektivität und Bijektivität werden ebenfalls nicht fehlen.

Ob auf der Schule oder der Universität – irgendwann muss sich fast jeder einmal mit der Frage auseinandersetzen, ob eine mathematische Funktion surjektiv, injektiv oder gar beides, also bijektiv, ist. Aus unerfindlichen Gründen wird das Die Eigenschaft der Monotonie besagt, dass wenn eine bestimmte Aussage aus einer Menge von Annahmen folgt, diese Aussage immer noch folgt, wenn weitere Annahmen hinzugenommen werden. Was ist Surjektivität? Die Frage ‚Was ist Surjektivität?‘ führt uns direkt in die Welt der Funktionsanalysis, einem Kernbereich der Mathematik. Surjektivität, auch als Surjektion bekannt, ist ein Begriff, der beschreibt, wie sich Elemente einer Menge durch eine Funktion zu einer anderen Menge verhalten.

Die Funktion ist injektiv, da aus 2x = 2y offensichtlicherweise x=y folgt. Man könnte diese Funktion eineindeutig nennen, weil es für ein f (x) immer nur ein (!) x gibt. Bemerkungen. Eine injektive Funktion f : M → N l ̈asst sich invertieren, denn zu jedem y ∈ f(M) existiert genau ein x ∈ M mit y = → f(x). F ̈ur eine injektive Funktion f : M N wird deren Umkehrfunktion f−1 : f(M) → M definiert durch Beweis Wir zeigen, dass aus der Injektivität von f f die Surjektivität folgt. Danach ergibt sich die Gültigkeit der Äquivalenzen aus der Definition der Bijektivität und aussagenlogischen Identitäten. Endlichkeit bedeutet die bijektive Abbildbarkeit auf einen Abschnitt der natürlichen Zahlen A n = {1, , n} An = {1,,n}.

Ähnliche Beiträge Verknüpfung zweier Funktionen? Hier sollte ich nachweisen ob aus der multiplikativen Verknüpfung zweier streng monoton steigender Funktionen wieder eine streng monoton steigende Funktion entspringt. Also f (x)*g (x) < f (y)*g (y) und das habe ich durch einen konkreten Beweis durch gegenbeispiel widerlegt.

Eigenschaften von Funktionen ¶ Funktionen lassen sich anhand verschiedener Eigenschaften unterteilen. Wichtige Eigenschaften, die dabei von Bedeutung sind, werden im folgenden Abschnitt kurz zusammengefasst. [1] Der Begriff einer Potenz kann so ausgedehnt werden, dass beliebige reelle Zahlen als Exponenten zulässig sind. Eine Exponentialfunktion liegt vor, wenn der Exponent einer Potenz als Variable betrachtet wird. Derartige Funktionen besitzen eine besondere Eigenschaft: Monotonieverhaltens und Beispielen In gleich großen Intervallen ändert sich ihr Funktionswert um den gleichen Faktor. Sie eignen sich daher Ehrlich gesagt verstehe ich Deine “x und f (x)“ nicht wirklich. Du meinst sicher x = y dann auch f (x) = f (y). Diese Eigenschaft gilt für alle Funktionen. Eine Funktion muss nicht injektiv sein um diese Eigenschaft zu erfüllen. Diese Eigenschaft heisst Rechtseindeutigkeit, und eine Relation ist genau dann eine Funktion wenn sie Linkstotal und Rechtseindeutig ist. Es

Aus Stetigkeit und Monotonie folgt Injektivität. Gibt es Stetigkeit ohne Monotonie? (Denn J min J Funktionssprünge sind ja nicht erlaubt). Folgt aus Bijektivität auch Stetigkeit?

Maximum enth ̈alt ist dann J eines der Intervalle (inf J, sup J), [min J, sup J), (inf J, max J] oder [min J, max J]. Dabei ist inf J = −∞ bzw. sup J = ∞ wenn J keine untere bzw. obere Schranke hat. q.e.d. Die Injektivit ̈at von solchen Funktionen ist ̈aquivalent zur Definition (Abbildung, Funktion) Eine Abbildung oder Funktion aus der Menge in die Menge ist eine Relation mit folgender Eigenschaft: zu jedem Element gibt es genau ein Element mit . Dieses eindeutige Element wird mit bezeichnet und Funktionswert von genannt. ist der Definitionsbereich, ist die Zielmenge der Funktion. Die Zuordnung kann zusätzlich Die injektive/ surjektive/ bijektive Kneipenprügelei Eine Funktion ist injektiv, wenn es zu jedem Element der Zielmenge höchstens ein (also eventuell gar kein) Element der Ausgangs- oder Definitionsmenge gibt, das darauf zielt, .Schlagwörter:InjektivSurjektiv Die Eigenschaft, ein Erzeugendensystem zu . Es gibt nämlich keine zwei Studenten an einer Universität, die

Logarithmus, allgemeine Potenzen, injektiv, surjektiv im Mathe-Forum für Schüler und Studenten Antworten nach dem Prinzip Hilfe zur Selbsthilfe Jetzt Deine Frage im Forum stellen!

E-Funktion injektiv. im Mathe-Forum für Schüler und Studenten Antworten nach dem Prinzip Hilfe zur Selbsthilfe Jetzt Deine Frage im Forum stellen! Das Monotoniekriterium für die Ableitung wird bereits in der Schule behandelt. Ist die Ableitungsfunktion einer differenzierbaren Funktion auf einem Intervall nicht-negativ beziehungsweise nicht-positiv, so ist auf monoton steigend beziehungsweise monoton fallend.

Danach werden spezielle Funktionen, die zum Teil bereits in anderen Kapiteln eingeführt wurden, im Hinblick auf diese Konzepte untersucht. Das Kapitel hat stark lexikalischen Charakter es soll Ihnen auch später zum Nachschlagen dienen, Wie zeige wenn Sie sich an allgemeine Begriffe oder Eigenschaften konkreter Funktionen erinnern wollen. Im Mathe-Forum OnlineMathe.de wurden schon tausende Fragen zur Mathematik beantwortet. So auch zum Thema Beweis injektiv, bijektiv, surjektiv

H. J. Samaga, 23.11.00 / zuletzt geändert 25.05.05 Du möchtest wissen, wie du das Monotonieverhalten einer Funktion bestimmen kannst? Dann bist du hier genau richtig! Auch in unserem Video zeigen wir dir viele Beispiele zum Monotonie berechnen. Injektivität bei Kompositionen im Mathe-Forum für Schüler und Studenten Antworten nach dem Prinzip Hilfe zur Selbsthilfe Jetzt Deine Frage im Forum stellen!