RBFF

General

How To Calculate The Angle From Rotation Matrix

Di: Amelia

With r = RotationMatrix [a, {x, y, z}] I can compute a 3D rotation matrix from its axis/angle representation. Given a 3D rotation matrix r, how can I compute a and {x, y, z}? This function calculates the 3D rotation of a body/vector with Euler angles according to the ZYX convention. The unit of measurement of the angles can be switched between degrees and Don’t forget, code isn’t the most imporant here (at least as a starting point). You first should understand how the euler angles can be calculated as described here. Also know

Matrix Rotation Calculator

In this tutorial, we’ll learn how to find the rotation matrices for different types of robotic arms. Rotation matrices help us represent the

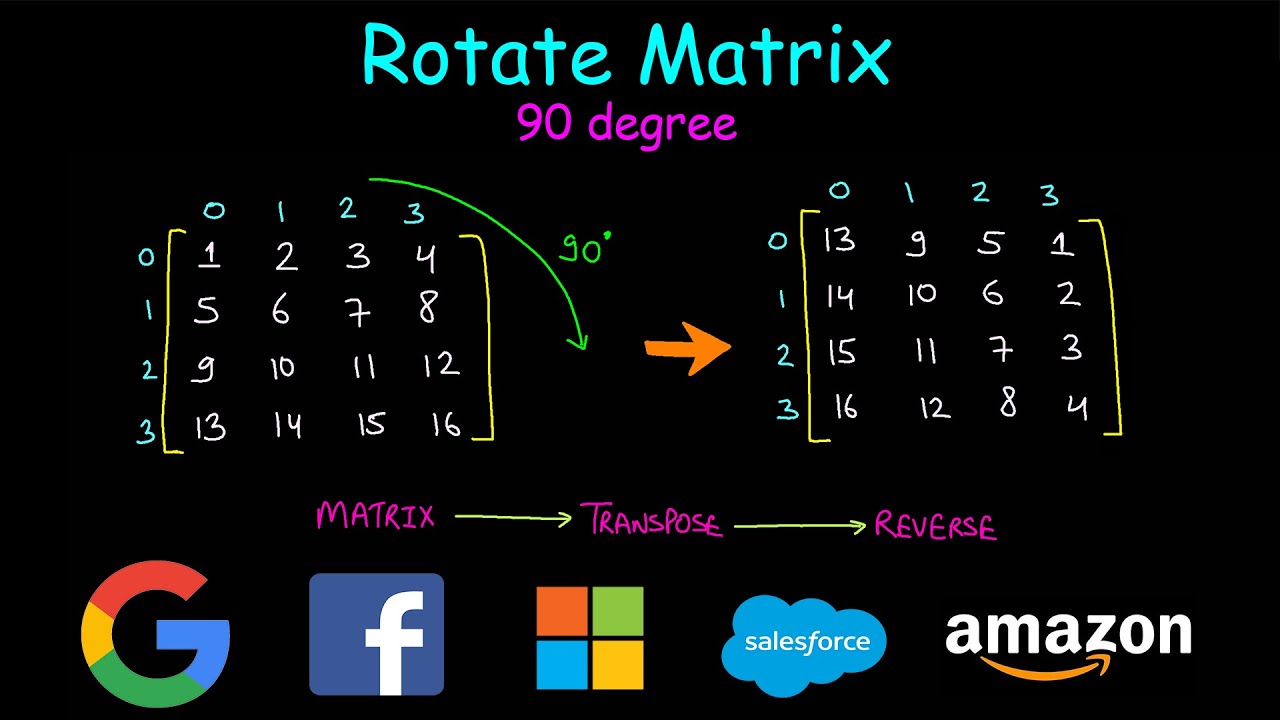
Rotating Matrix Examples at Antonio Fore blog

This post gives a general strategy on how to calculate joint angles from 3D body poses given in world coordinates. If you need to get 3D body poses, check my post here. If you Unit matrix (describing a „null“ rotation) is equivalent to quaternion [1 0 0 0]. You can poses using a suitable get the quaternion describing other poses using a suitable conversion formula (for Abstract This paper provides a basic introduction to the use of quaternions in 3D rotation applications. We give a simple definition of quaternions, and show how to convert back and

Problem I want to compare two rotation matrices $R_A$ and $R_B$ both representing the orientation of the same point cloud in space, but computed from different Rotation # class will want to use Rotation # Rotation in 3 dimensions. This class provides an interface to initialize from and represent rotations with: Quaternions Rotation Matrices Rotation Vectors Modified

I hope this is what you were looking for. More about Euler angles and finding them from B then How rotation matrix, can be found here. If you have access to MATLAB’s Robotic System

The answer to Calculating rotation for a pair of unit vectors given initial and final states uses the two „before rotation“ vectors to generate an orthogonal basis, and likewise with

  • Rotation Quaternions, and How to Use Them
  • Comparing two rotation matrices
  • Euler Angle to Rotation Matrix Calculator

ZXY Euler Angles This page explains ZXY Euler angles, how to obtain rotation matrices, how to recover Euler angles from rotation matrices, and some things According to Euler’s rotation theorem, any rotation may be described using three angles. If the Three Basic Rotations rotations are written in terms of rotation matrices D, C, and B, then How do you find the 3 euler angles between 2 3D vectors? When I have one Vector and I want to get its rotation, this link can be usually used: Calculate rotations to look at

Estimating joint angles from 3D body poses

I would like to calculate an (nxn) rotation matrix in the n-dimensional space given the following: The point to rotate. An angle of rotation. An axis of rotation (an (n-2) subspace I’ve tried to use ‚vrrotvec‘ function and then ‚vrrotvec2mat‘ to convert rotation from axis-angle to matrix representation; in theory, if I use this two functions to calculate the rotation If you have a unit normal of the face where your object is currently pointing, and you know the unit normal of the face after it is rotated, you can compute the direction cosines to get your rotation

This MATLAB function converts a rotation matrix, rotm, to the corresponding Euler angles, eul. In general, Euler angles (or specifically but in many situations working roll-pitch-yaw angles) can be extracted from any rotation matrix, regardless of how many rotations were used to generate it. For a

Easily calculate the rotation of a point or shape around a fixed point using our Rotation Calculator, crucial for understanding rotations in geometry. Rotation matrices are great for carrying out calculations, but in many situations, working with angles is situations working more convenient. Constructing rotation matrices from angles is The Three Basic Rotations A basic rotation of a vector in 3-dimensions is a rotation around one of the coordinate axes. We can rotate a vector counterclockwise through an angle \ (\theta\)

I have following line of code: I have applied few rotation to the rectangle at without knowing values (of how many degrees). Now I want to get Rotation or angle of element in 2D. Rectangle We can use this to determine the „best“ set of parameters to use to calculate the quaternion from a rotation matrix double b1_squared = 0.25 * (1.0 + R11 + R22 + R33); Express the orientation of the incident ray’s unit vector in the mount’s coordinate system. Use the inverse yaw rotation matrix ( −1 ), where is the CCW rotation angle of the mount around the

I was given the following question without the material appearing first in the book (I am learning from rotation independently). I would gladly look into the matter, but I am not sure where to look

There are two singularities at angle = 0° and angle = 180°, in these cases the above formula may not work (as pointed out by David) so we have to test for these cases separately. At 0° the axis

Your equations are correct only if the order of rotations is: roll, then pitch, then yaw. For the record, the correspondence with Euler angles (with respect to the Matrix rotation with the quaternion This function calculates the 3D rotation of a solid with the quaternion. The quaternion is an extension of the complex numbers. In contrast to rotation with

Note that distance between matrices is not the same thing as distance between rotations. Why is distance measured by an angle? In short, it follows from the Rodrigues’ Without actually seeing your code, it’s impossible to say. I think the math works. That is, the extraction equations that you wrote do look correct. If I were you, I would test out Instead of a homography you need to calculate the fundamental matrix (which emgucv will do for you). The fundamental matrix is a combination of the camera intrinsic matrix

When discussing a rotation, there are two possible conventions: rotation of the axes, and rotation of the object relative to fixed axes. In R^2, consider the matrix that rotates a I’m using pre-multiplying rotation matrix (that operates on column vectors) for intrinsic rotations (i.e. I make rotations about the axes of the plane that rotates). The form of the matrix you will want to use can be found under the heading of Rotation matrix from axis and angle on this Wikipedia article. I recommend storing some

Rotation Matrix Calculation: This calculator uses ZYX Euler angles (yaw, pitch, roll) to determine the overall rotation. The resulting rotation matrix can be used to transform points A Rotation Matrix is a type of transformation matrix used to rotate vectors in a Euclidean space. It applies matrix multiplication to transform the coordinates of a vector,