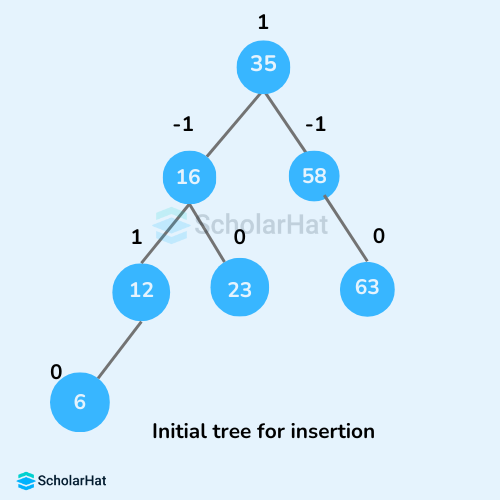
How To Insert A Node In An Avl Tree

Di: Amelia

Otherwise: If the value to insert matches the current node, do nothing. Otherwise, recursively insert the node into the proper subtree and get the amount that the tree height has changed by. Update the balance factor of this node based on the amount that the subtree height changed. If this mandates a series of rotations, perform them. This rotation is performed when a node has a balance factor as +2, and its left-child has a balance factor as -1. Insertion in AVL Trees Insert operation is almost found in the the same as in simple binary search trees. After every insertion, we balance the height of the tree. Insert operation takes O (log n) worst time complexity. Create the AVL tree from the sorted array by following the approach described here. Now, find the level order traversal of the tree which is the required sequence. Adding numbers in the sequence found in the previous step will always maintain the height balance property of all the nodes in the tree. Below is the implementation of the

An AVL tree is a self-balancing binary search tree where the height difference between the left and right subtrees of any node is at most one, ensuring efficient operations. One consequence of this is the double rotate cases below require inserting an extra node to keep the tree balanced after inserting the node to be deleted. This results in the insert case tree of height not being minimal. In other words, if i add a key with the number 4 (key = 4), I can make an Insert to another key with the number 4 (another key = 4). Eventually my tree would be, X in root, left sub tree has values less than X, right sub tree has values greater or EQUAL to X. (Or obviously can allow the EQUAL to the left sub tree instead to the right).

AVL Tree in Data Structures with Examples

AVL property: 1 balance(x) 1, for every node x Ensures small depth Will prove this by showing that an AVL tree of height must have a lot of (*roughly* 2h) nodes

How many rotations after AVL insertion and deletion

Inserting an element on a B-tree consists of two events: searching the appropriate node to insert the element and splitting the node if required.Insertion operation always takes place in the bottom-up approach. Let us understand these events below. When we insert a new node into our AVL tree that causes an imbalance in a subtree, our tree will do a left or right rotation at the imbalanced node as needed to balance the tree.

Animation showing the insertion of several elements into an AVL tree. It includes left, right, left-right and right-left rotations. Fig. 1: AVL tree with balance factors (green) In computer science, an AVL tree (named after inventors A delson- V elsky and L andis) is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if If after an insertion, the AVL tree becomes imbalanced: Find the first imbalanced node from the point of insertion (Recall that only node from inserted node ⇒ root can become imbalanced): Apply the (appropriate for that configuration)) tri-node reconstruction operation on the tree rooted at the first imbalanced node = x: The tree class should include a root node, which will be used to point to the root node of the AVL Tree. The tree class should also include methods to perform operations on the tree, such as insert, search, and delete.

I was doing some research about AVL trees, and i got to know that the insertion order matters in AVL trees. But i didnt find something that could clarify me whats the best way to know which is the correct insertion order in a AVL tree. for example: I have to insert 1 2 3 4 5, how do i know which is the best way to insert and why?

AVL tree stands for Adelson-Velsky and Landis tree. An AVL tree is a type of self-balancing binary search tree. In an AVL tree, the height of two child subtrees of any of the nodes differs by no more than one, ensuring that the tree remains balanced. This property helps in maintaining the tree’s height to O (log n), which ensures efficient operations such as search 3. How to Balance an AVL Tree? The AVL Tree checks the balance factor of its nodes after the insertion or deletion of a node. If the balance factor of a node is greater than one or less than -1, the tree rebalances itself. There are two operations to rebalance a tree: right rotation and left rotation. 3.1. Right Rotation Let’s start with the right rotation. Assume we have

AVL Tree in Python: Complete Guide

Understanding and Implementing AVL Trees
AVL Tree: A tree that can stay balanced by rotating
AVL Trees: A Complete Guide
AVL Tree in Python: Complete Guide

Insert nodes accordingly: To make sure that the given tree remains AVL after every insertion, augment the standard BST insert operation to perform some re-balancing. I’m having the hardest time trying to figure out how to balance an AVL tree for my class. I’ve got it inserting with this: Node* Tree::insert (int d) { cout << "base insert\t" << d Can you solve this real interview question? Insert into a Binary Search Tree - You are given the root node of a binary search tree (BST) and a value to insert into the tree. Return the root node of the BST after the insertion. It is guaranteed that the new value does not exist in the original BST. Notice that there may exist multiple valid ways for the insertion, as long as the tree remains a

Worst-case left-heavy AVL trees Looking at the total number of nodes in the tree we see that for a tree of height 0 there is 1 node, for a tree of height 1 there is 1 + 1 = 2 1+1=2 nodes, for a tree of height 2 there are 1 + 1 + 2 = 4 1+1+2=4 and

When inserting a new node in an AVL tree, normal binary search tree insertion rules apply. We start from root, recursively traverse left or right subtree based on the new value to be inserted the level order traversal until we reach a leaf node. Deleting a node from an AVL tree is similar to that in a binary search tree. Deletion may disturb the balance factor of an AVL tree and therefore the tree ne

Is it true that inserting an element to an AVL tree requires $O(1)$ rotations? How many rotations, does deletion from AVL require? I’ve searched for these two Insertion operation The data is inserted into the AVL Tree by following the Binary Search Tree property of insertion, i.e. the left subtree must contain elements less than the root value and right subtree must contain all the greater elements. However, in AVL Trees, after the insertion of each element, the balance factor of the tree is checked; if it does not exceed 1, the tree is left as it In this article, we will discuss insertion in AVL Tree using Java. AVL tree is created and the difference of height is printed for each node.

How to implement insertion for AVL tree without parent pointer?
AVL Tree in Python: Insertion, Deletion & Rotation
How many rotations after AVL insertion and deletion
AVL Tree: Complete Guide With Python Implementation
Insertion in AVL Tree In C++

I saw some articles about the implementation of AVL’s rebalance() function. After each insertion, we should check the insertion Node’s ancestors for balance. So I think, in order to check ancestors‘ I’m trying to implement an AVL TREE and I stumble upon this problem, how to update the height whenever I insert a new node? I know that I have to update the height of the node all the way up.

Insertion In AVL Tree AVL tree is self balancing tree in which for all nodes, the difference of height between the left subtree and the right subtree is less than or equal to 1. In this article, an avl tree is created and the difference of height is

CSE 332: Data Structures & Parallelism Lecture 8: AVL Trees

I’m currently trying to implement an AVL tree in C++, so far I’ve done pretty much everything except a node removal. 1) Can someone confirm that my algorithm for removing a node is correct? balance factor of an AVL Find the node to delete in the tree if the node has 0 child : delete the node else, if the node has 1 child: delete the node, and re-link his child else (2 children): find its successor,

Learn how to implement AVL Tree in Python and how to perform insertion and deletion. Also, what are its advantages and disadvantages? For both operations – inserting or deleting of a node x, there are cases that require rotations the hardest time trying to be made on all nodes from x up to the root. Since height of a tree with n nodes is O (log n), the worst case for both operations take O (log n) rotations. For n insert/delete operations that gives O (n log n).

An AVL Tree (Adelson-Velsky and Landis tree) is a self balancing binary search tree such that for every internal node of the tree the heights of the children of node can differ by at most 1. It uses four types of rotations to keep itself balanced and delete, insert and search take O(log N) time Binary Search Tree A Binary Search tree has the following property: All nodes should be such that the left child is always less than the parent node. The right child is always greater than the parent node. In the following sections, we’ll see how to search, insert and delete in a BST recursively as well as iteratively.

Inserting the element in the AVL tree is same as the insertion performed in BST. After insertion, check the balance factor of each node of the resulting tree. After the insertion, the balance factor of each node is either 0 or 1 or -1, then the tree is considered to be balanced, concludes the operation, and inserts the next element if any.

RBFF

General