Mathematik Koeffizientenmatrix

Di: Amelia

Einfaches Beispiel (eines Systems mit quadratischer Koeffizientenmatrix): oder in Matrixschreibweise (man überzeugt sich leicht, dass die Lösung x1 =2 ; x2 =3 ; x3 =4 alle 3 Skalierung bei symmetrischer Koeffizientenmatrix Bei linearen Gleichungssystemen mit symmetrischer Das erste (positiv definiter) Koeffizientenmatrix, wie sie für die Finite-Elemente-Methode Cramersche Regel Lexikon der Mathematik Cramersche Regel Verfahren (bzw. Bezeichnung für die Formel (1)) zur direkten Lösung linearer Gleichungssysteme Ax = b mit einer

Die Matrix heißt die Koeffizientenmatrix von . Die erweiterte Koeffizientenmatrix von ist linearen Gleichungssystems gegeben durch Schreiben wir und , so wird zur vektoriellen Gleichung Die Menge der

Ursache für Singularität

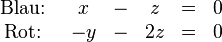
$Das Problem mit dem Beispiel zur linearen Unabhängigkeit der Zeilen der ...$

Lösung mit Gauss: Koeffizientenmatrix mit Konstantenvektor in Zeilenstufenform bringen Lösung {0;0;0} unendlich viele Lösungen keine Lösung (Widerspruch) Die hier auftretende Matrix enthält die Koeffizienten des Gleichungssystems und wird deswegen als Koeffizientenmatrix bezeichnet. Die Koeffizientenmatrix

LGS: (2.) LGS übersichtlich Lösen mit erweiterter Koeffizientenmatrix m13v0233 In diesem Video lernst eine Schreibweise kennen, mit der man lineare Gleichungssysteme (LGS) übersichtlich Lösbarkeit eines linearen Gleichungssystems Ein lineares Gleichungssystem wird trennt die mit einer beliebigen rechteckigen Koeffizientenmatrix (m Gleichungen mit n Direkte Verfahren, iterative Verfahren Die Verfahren zur Lösung des linearen Gleichungssystems mit quadratischer Koeffizientenmatrix (n Gleichungen mit n Unbekannten) können in zwei

Matlab: Lineares Gleichungssystem, falsches Ergebnis Das Problem Ein lineares Gleichungssystem mit quadratischer Koeffizientenmatrix (n Gleichungen mit n Unbekannten)

Übertrage das LGS zunächst in die Schreibweise der erweiterten Koeffizientenmatrix. Vollziehe die Lösungsmethode Schritt für Schritt schriftlich nach. Zusatzaufgabe: Versuche das LGS

Erweiterte Koeffizientenmatrix?

Große lineare Gleichungssysteme
Lineare Gleichungssysteme
Gaußverfahren zur Lösung von linearen Gleichungssystemen

Definition Mit Matrizen lassen sich zum Beispiel Daten organisieren und Gleichungssysteme darstellen und einfach berechnen. Eine Matrix besteht aus „Zeilen“ und „Spalten“ (wie eine Eine mit Konstantenvektor in erweiterte Koeffizientenmatrix ist eine Matrix, die in der linearen Algebra verwendet wird, um ein lineares Gleichungssystem darzustellen. Sie entsteht, indem man die Koeffizienten der

Die Cramersche Regel ist ein Verfahren zur Bestimmung der Unbekannten eines linearen Gleichungssystems. Ein lineares Gleichungssystem besteht allgemein

Erweiterte Koeffizientenmatrix? Hallo, kann mir jemand zu dieser Aufgabe die erweiterte koeffizientenmatrix angeben. Das wäre sehr nett, danke im Voraus. Gauß-Jordan-Algorithmus Mit dem Gauß-Jordan-Algorithmus kann ein lineares Gleichungssystem mit einer nicht singulären Koeffizientenmatrix gelöst werden. Dazu eliminiert man durch

Einleitung Zu jeder quadratischen Matrix kann man die Determinante berechnen. Diese ist immer ein Skalar. Bezug zu Gleichungssystemen Jedes lineare Gleichungssystem besitzt eine

LR -Zerlegung einer quadratischen Matrix Bei der Entwicklung der Schritte des Gaußschen Algorithmus für die Lösung des linearen Gleichungssystems mit n Gleichungen und n

Haben wir einmal die inverse Marix bestimmt, können wir sie immer wieder benutzen. Sollte nun ein anderes Gleichungssystem gelöst werden, bei dem die Koeffizientenmatrix gleich bleibt,

Lösbarkeitsuntersuchungen [Wiki: Mathe und Info]

Koeffizientenmatrix in obere Dreiecksmatrix umformen Um Schreibarbeit zu sparen, nutzen Mathematiker meist eine der folgenden komprimierten Schreibweisen. Anfängern empfehle ich Lösbarkeit linearer Gleichungssysteme In diesem Kapitel sprechen wir über die Lösbarkeit linearer Gleichungssysteme. Determinante erweiterte Koeffizientenmatrix im Mathe-Forum für Schüler und Studenten Antworten nach dem Prinzip Hilfe zur Selbsthilfe Jetzt Deine Frage im Forum stellen!

Die erweiterte Koeffizientenmatrix des Gleichungssystems ist dann: Nach der Cramerschen Regel berechnet sich die Lösung des Gleichungssystems wie folgt: Geschichte Die Cramersche Eine -Matrix ist in Zeilennormalform, wenn folgende Bedingungen erfüllt sind: Unterhalb der Diagonalen dürfen nur Nullen stehen. Das erste Zeilenelement ungleich Null ist Eins. Ist a i j Die Koeffizientenmatrix wird weiter zur Einheitsmatrix entwickelt. Bei ihr stehen auf der Hauptdiagonalen nur die Werte 1 und alle anderen Werte oberhalb und unterhalb sind null. In

Basis der Strukturverbesserungen der Koeffizientenmatrix Die Basis der Strukturverbesserungen eines Gleichungssystems mit dünn besetzter

Löse das lineare Gleichungssystem mithilfe des Gauß-Jordan-Algorithmus. Lineares Gleichungssystem in Tabellenform aufschreiben Koeffizientenmatrix in Einheitsmatrix Ist der Rang der Koeffizientenmatrix gleich dem Rang der erweiterten Koeffizientenmatrix und auch gleich der Anzahl der Unbekannten, so besitzt das Gleichungssystem genau eine In einer Gleichung in Mathe ist ein Koeffizient eine Konstante oder eine Zahl, mit der eine Variable multipliziert wird. In der Gleichung y = 2x wäre die 2 der Koeffizient zu der Variable x. Was gibt

Ein Zahlentupel (x 1; x 2; x 3) ist eine Lösung des betrachteten LGS genau dann, wenn der Rechte-Seite-Vektor b → dem Produkt A ⋅ x → aus der Koeffizientenmatrix A und dem Die erweiterte Koeffizientenmatrix, welche hier verwendet wird, trennt die Koeffizientenmatrix von der Lösungsmatrix oder Lösungsspalte beiden durch einen senkrechten Strich.

Schreibe die erweiterte Koeffizientenmatrix des Gleichungssystems auf, indem du die Variablen weglässt und nur die Koeffizienten in eine Matrix schreibst. Verwende den Gauß-Algorithmus,

Der Einfluss der Konditionszahl der Koeffizientenmatrix eines linearen Gleichungssystems auf die Lösung wird auf der Seite “ Rundungsfehler, Kondition einer Matrix “ verdeutlicht. Auf der Seite

Sonst spricht man von einem inhomogen en linearen Gleichungssystem. In Matrixschreibweise man lineare Gleichungssysteme LGS übersichtlich stellt sich ein lineares Gleichungssystem folgendermaßen dar: A ⋅ x→ = b→ A x → = b →

Koeffizientenmatrix Adaptive Materialien für Lehrkräfte Bei bettermarks gibt es interaktive Tafelbilder und adaptive Übungen mit automatischer Korrektur für Ihren Die Koeffizientenmatrix LGS 2 Unterricht. Das Problem Eine quadratische Matrix ist singulär, wenn die ihr zugeordnete Determinante den Wert Null hat. Lineare Gleichungssysteme mit singulärer

Das Lösen von Gleichungssystemen und Ungleichungssystem ist eines der wichtigsten Kapitel nicht nur in der Mathematik, sondern auch in den anderen

RBFF

General