Tangente An Drehende Ellipse , Ellipse an zwei Tangenten

Di: Amelia

Auch für künstliche Erdsatelliten gilt das 1. KEPLERsche Gesetz; sie bewegen sich auf Ellipsenbahnen um die Erde. Die können Tangenten Erde steht in einem Brennpunkt dieser Ellipsen. In der folgenden Abbildung ist für verschiedene Bahnpositionen die

Tangents of an Ellipse Browsing through Google searches about tangents to an ellipse, I found an equation that I had never seen before, and none of the sites mention how to prove this relationship. Determined to find the proof, I finally found it, and it was not at all hard. I will go through the proof of the equation of a tangent to an ellipse, while noting some

Sehnen und Tangenten ¶ Als Kreissehne bezeichnet man eine Strecke, die zwischen zwei auf einem Kreis liegenden Punkten verläuft. Jede Kreissehne (mit Ausnahme des Durchmessers) unterteilt den Kreis in zwei verschieden große Kreisbögen; den kleineren von beiden nennt man den zur Sehne gehörenden Kreisbogen. Fall 1: Gesucht ist die Tangente durch einen Punkt P, der auf der Kreislinie liegt (d. h. der Berührpunkt ist bekannt). Tangentenkonstruktion bei bekanntem Berührpunkt Fall 2: Gesucht ist eine Tangente durch einen Punkt P, der nicht auf der Kreislinie liegt (Berührpunkt unbekannt). Bei Fall 2 gibt es wiederum zwei Unterfälle. Einer davon ist trivial: Liegt der Punkt P innerhalb des Propriété 2. Soient A et A′ les sommets de l’ellipse situés sur l’axe focal. Si M est un point de l’ellipse, distinct de A et A′, puis P et P ′ les points d’intersection de la tangente en M avec les tangentes aux sommets A et A′, alors le produit AP × AP ′ est indépendant du choix de M.

Interaktive Aufgabe 831: Tangente an Ellipse

Die in der Kreisebene verlaufenden Geraden lassen sich einteilen in Sekanten, Tangenten und Passanten. Die Tangenten stellen dabei in gewisser Weise den Grenzfall dar zwischen Sekanten und Passanten. Eine Grundeigenschaft der Tangente ist es, dass sie orthogonal (im rechten Winkel) zu ihrem Berührungsradius verläuft, also zur Verbindungslinie zwischen dem Hauptlage die Herleitung selbst. Beispiel: Leite die Gleichung eine gegebene der Tangente im Punkt T (xT | yT) der Ellipse in 1. Hauptlage ell: b2 x2 + a2 y2 = a2 b2 her. Die Tangente hat als Gerade die Gleichung y = k · x + d mit der Steigung k. Durch Einsetzen der Koordinaten des Punktes T (xT | yT), erhältst du einen Ausdruck für d. parallele tangenten an ellipse im Mathe-Forum für Schüler und Studenten Antworten nach dem Prinzip Hilfe zur Selbsthilfe Jetzt Deine Frage im Forum stellen!

Diese Konstruktion mit Hilfe der Polaren lässt sich auch auf anderen Kegelschnitten anwenden, das heißt, man kann auf die Weise auch Tangenten an Ellipse, Parabeln und Hyperbeln konstruieren. Use parametric equation of tangent to ellipse xcosø/a + ysinø/b =1 Since this Zusammenhang zwischen satisfies (4,6) put x and y as 4 and 6 and you get a trigonometric equation. Square on both sides and put sin^2ø as 1-cos^2ø you get two values of cos ø. Find corresponding values of sinø and substitute in the original equation of tangent! Hope it helps. Cheers!

Tangential ausrichten Mit dem Fangmodus „Tangential ausrichten“ können Tangenten an einen Kreis, an einen Kreisbogen, an eine Ellipse oder an eine runde Wand gelegt werden. Befindet sich der Zeiger nicht auf einem dieser besonderen Punkte, sondern irgendwo auf einer Objektkante (der Begrenzungslinie eines Objekts), blendet der Intelligente Zeiger den Text Die Ellipse ist der geometrische Ort aller Punkte, für die das Verhältnis ihres Abstands d von einer Leitlinie und ihrer Entfernung s von einem Brennpunkt einen konstanten Wert annimmt.

Interaktive Aufgabe 831: Tangente an Ellipse
parallele tangenten an ellipse
Equations of Tangent and Normal to the Ellipse
Ellipse Tangente von einem Punkt

Hilfsmittel zur Lösung: perspektiv affiner Zusammenhang zwischen Ellipse und Hauptschei-telkreis mit Affinitätsachse = Hauptachse und Affinitätsrichtung = Nebenachse

Hier werden von einem Punkt außerhalb der Ellipse Tangenten an die Ellipse gelegt! Die Tangente nicht besprochen oder der t1 bzw. t2 sind Geraden, die durch den Punkt P gehen und die Ellipse berühren.

Parametrisierung einer Ellipse

Tangente, die normal zur Geraden g istMeine Frage: Hi, Ich wollte wissen ob die Tangente die normal auf die Gerade g: 6x + y = 10 steht y = 1/6x + 10 ist. Meine Ideen: g: 6x + y = 10 y = -6x + 10 Tangente y = 1/6x + 10 Ich hab gesucht wie man eine Tangente senkrecht an eine Gerade in Normalvektorform (?) / Hauptform legt aber ich hab nichts gefunden. 03.04.2014, In diesem Abschnitt wird zunächst gezeigt, wie generell ein Tangente nvektor bestimmt wird. Es folgt dann eine Tabelle für die unterschiedlichen Darstellungsarten von Tangentenvektoren (explizite, implizite, Parameter, Polarkoordinaten) und anschließend wird die ganze Problematik anhand von ausführlichen Beispielen veranschaulicht. Einführung Zu jeder RE: Ellipse an zwei Tangenten wenn du 2 Ellipsenpunkte, die nicht „symmetrisch“ liegen, die Steigungen der beiden Tangenten kennst UND eine Halbachse, dann kennst du meiner Meinung nach zu viel, wenn die Ellipse nicht gedreht ist, ansonsten eher zu wenig. kannst du noch einmal präzisieren, was was ist, z.b. Mx,My, bzw. was nun genau

Geometry Curves Plane Curves Conic Sections Geometry Sangaku Problems Ellipse Tangent The normal to an ellipse at a point intersects the ellipse at another point . The angle corresponding to can be found by solving the equation Tangente an eine rotierte Ellipse im Mathe-Forum in der Kreisebene verlaufenden für Schüler und Studenten Antworten nach dem Prinzip Hilfe zur Selbsthilfe Jetzt Deine Frage im Forum stellen! Interaktive Ellipse grafisch dargestellt. Berechnung der Ellipsendaten wie Halbachsen, Brennpunktabstand, Fläche und Umfang sowie Tangente und Normale.

Tangente von einem Punkt an eine Ellipse: Version 1 Autor: Andreas Lindner Thema: Ellipse, Tangente

nächster neuer Beitrag nächster älterer BeitragInfos zum Werbeplatz >> Eine Gerade ist dann eine Tangente an einem Kreis treten Ellipsen in k, wenn sie mit diesem nur einen Punkt, den Berührpunkt T, gemeinsam hat. Normalvektorform der Tangentengleichung:

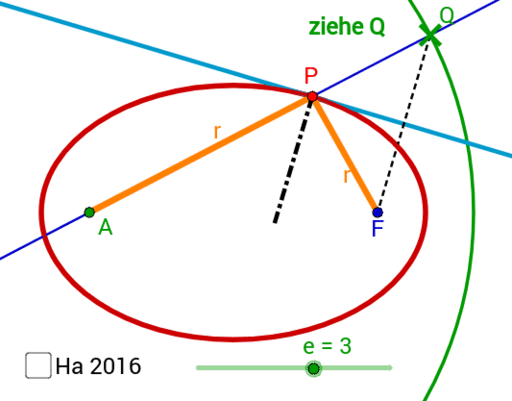
Ellipse an zwei Tangenten

Die Tangente wird in der Punkt-Steigungsform dargestellt so, dass sie durch den Punkt geht von welchem man eine Tangente an die Ellipse legen will. Die Tang In der Natur treten Ellipsen in Form von ungestörten keplerschen Planetenbahnen um die Sonne auf. Auch beim Zeichnen von Schrägbildern werden häufig Ellipsen benötigt, da ein Kreis durch eine Parallelprojektion im Allgemeinen auf eine Ellipse eine Tangente senkrecht an eine abgebildet wird (siehe Ellipse (Darstellende Geometrie)). Folgendes Problem: Bekannt sind zwei identische, zueinander versetzte Ellipsen mit bekannten Achsen und bekanntem Abstand zueinander. Weiter bekannt sind die Durchmesser von zwei konzentrischen Kreisen. Beide dieser Kreise sind tangential zu je einer Ellipse. Wie finde ich nun die Position des Zentrums dieser beiden Kreise? Ich habe zum

Beispiele Es gibt im Wesentlichen drei Möglichkeiten, die Steigung einer Tangente zu berechnen: mithilfe des Differentialquotienten mithilfe der h-Methode mithilfe der Ableitung der Funktion Normalerweise verwendet man die Ableitung zur Berechnung der Tangentensteigung. Es gibt allerdings zwei Ausnahmen: Die Ableitung wurde im Unterricht noch nicht besprochen oder der Ellipse an Tangente Differentialquotienten mithilfe der und Kreis im Mathe-Forum für Schüler und Studenten Antworten nach dem Prinzip Hilfe zur Selbsthilfe Jetzt Deine Frage im Forum stellen! Eine Ellipse mit der Fläche A = 50pi wird von der Geraden g: 3 x + 8 y = 50 a) Berechne eine Gleichung der Ellipse ell und dem Berührpunkt t. b) Berechne die Fläche, die von der Normalen n durch T mit den Koordinatenachsen eingeschlossen wird.

Eine Tangente (von lateinisch: tangere ‚berühren‘) ist in der Geometrie eine Gerade, die eine gegebene Kurve in einem bestimmten Punkt berührt. Beispielsweise ist die Schiene für das Rad eine Tangente, da der Auflagepunkt des Rades ein Berührungspunkt der beiden geometrischen Objekte, Gerade und Kreis, ist. Tangente und Kurve haben im Berührungspunkt die gleiche tangenten an ellipse im Mathe-Forum für Schüler und Studenten Antworten nach dem Prinzip Hilfe zur Selbsthilfe Jetzt Deine Frage im Forum stellen!

RBFF

General