RBFF

General

Understanding 45-45-90 Triangles

Di: Amelia

A 45-45-90 triangle is a special type of right triangle where the two smaller angles are each equal to 45 degrees, and the third angle, which is the right angle, measures 90 degrees. Special Right Triangles Show and Explain all work for each problem. Each solution and work should demonstrate your understanding of Special Right Triangles (30 – 60 – 90 and 45 – 45 – Example 1: 45-45-90 Triangle Example 2: 30-60-90 Triangle How to Use “Special Right Triangles Calculator” Understanding the Input Fields How to Interpret the Results Practical Applications

The hypotenuse of a 45°-45°-90° triangle measures 18 cm.

Using these triangles allows us to solve problems without using the pythagorean not only theorem or trigonometric functions. Instead, we are able to rely on the known

45 45-90 triangles | PPTX

Our tool, the 45 45 90 Triangle Calculator, simplifies the complex calculations associated with 45 solve a missing side 45 90 triangles. It not only saves your time but also helps in understanding the principles of

Special right triangles are right-angle triangles with degrees of 30-60-90 or 45-45-90. Get he free printable worksheet as a DOC or a PDF. Use our free 45-45-90 Triangle Calculator to quickly compute side lengths, angles, area, and other properties of isosceles right triangles. Perfect for math students and educators. The content and examples cover isosceles right triangles with leg lengths of 45-45-90 degrees and 30-60-90 degree triangles. Formative assessments involve grouping students to solve

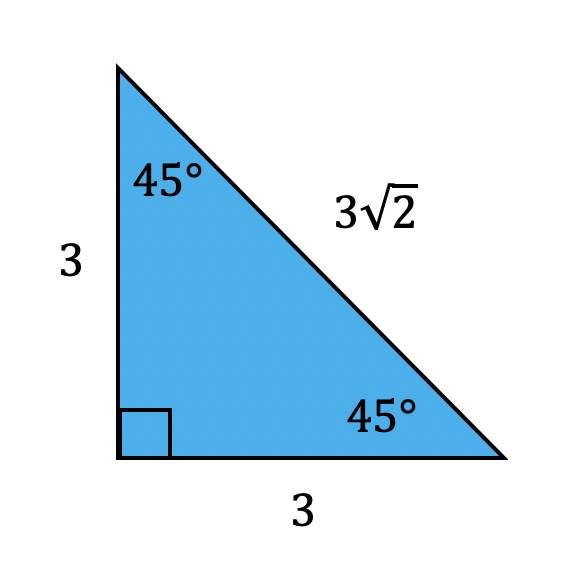
45-45-90 right triangle has side lengths of x, x, and x√2 30-60-90 right triangle has side lengths of x, x√3, and 2x In order to solve the problems on our special right triangles worksheets, you 3. Importance of 45-45-90 Triangle Calculations Calculating the properties of a 45-45-90 triangle is crucial for: Geometry Education: Understanding special triangles and their properties.

Special Right Triangle Theorem: 45-45-90 #Mathematics9

  • 45-45-90 triangle theorem
  • Special Right Triangle Theorem: 45-45-90 #Mathematics9
  • DLL Special Right Triangles

45 45 90 triangle calculator is a dedicated tool to solve this special right triangle. Find out what are the sides, hypotenuse, area, and perimeter of your shape and learn about the 45 45 90 triangle 45 45 90 Triangles QuickNotes In this lesson, you will learn about 45-45-90 triangle and what specific type of triangle is this. You will also learn about the relationship between the sides and how to solve a missing side.

Lesson 7.1-45°,45°,90° Triangles QuickNotes Check Your Understanding 1. Solve for the missing sides in each triangle. b. a. 2. If the hypotenuse of an isosceles right triangle is 20, what are the Although all right triangles have special features – trigonometric functions and the Pythagorean theorem. The most frequently studied right triangles, the special

The given triangle is an isosceles right triangle, also known as a 45-45-90 triangle. In this type 45 45 90 Triangle worksheets of triangle, two of the angles are equal at 45 degrees each, and the third angle is a right angle,

45°-45°-90° Triangles

Visualizing the Relationships To better understand these relationships, let’s visualize a 30-60-90 triangle: Applications of 30-60-90 Triangles 30-60-90 triangles are widely used in various fields,

Special Right Triangles Worksheets—Printable — Mashup Math

This video will help you to analyze the figure, label the angles, label the sides, and then understand the 30°-60°-90° and 45°-45°-90° triangles and find the labeled parts of each

The 45-45-90 triangle theorem states that in an isosceles right triangle, the angles measure 45 degrees, 45 degrees, and 90 degrees, and the lengths of the legs are equal while the length of Students will be able to understand the relationships between the side lengths in 30-60-90 and 45-45-90 triangles, find missing sides and perimeters in 30-60-90 and 45-45-90 triangles

The lesson plan covers teaching students about 45-45-90 special right triangles. The objectives are for students to illustrate, prove, and solve problems involving these triangles. Key concepts Right triangles are central to trigonometry. There are two special right triangles appear over and over in standardized exams and homework problems.

About 30-60-90 Triangles The 30-60-90 triangle is one of the most important special right triangles in geometry, alongside the 45-45-90 triangle. Its fixed angle Special main goals in this right triangles, namely the 30°-60°-90° and the 45°-45°-90° triangles, hold a unique place in the world of geometry. Their consistent internal relationships make them

  • 45-45-90 Triangle Calculator
  • What is the ratio of the sides of a 45-45-90 triangle?
  • Printable Grade 9 45 45 90 Triangle Worksheets Download
  • Your Comprehensive Tool: The 45 45 90 Triangle Calculator
  • Solve 30°-60°-90° and 45°-45°-90° triangles easily!

? Dive into the world of special right triangles, uncovering their unique attributes and learning strategies to solve them with ease in this comprehensive guide. Master the 45-45-90 and 30

Understanding 45°-45°-90° Triangle Theorem: In a 45°-45°-90° triangle, both legs are equal in length, and the length of the hypotenuse is 2 times the length of one leg. Learn to find the sine, cosine, and tangent of 45-45-90 triangles and also 30-60-90 triangles. 45 45 90 Triangle worksheets curated by Worksheetzone Discover the power of 45 45 90 Triangle Worksheets, thoughtfully crafted for teachers, homeschoolers, and parents who want

In a 45-45-90 right triangle, the two legs are of equal length, leading to a ratio of 1: 1. Therefore, the correct answer is option A. This demonstrates the properties of isosceles right Solve 45-45-90 triangle dimensions. Calculate sides, area, perimeter, and see steps with this simple triangle calculator and geometry helper.

In a 45-45-90 triangle, the angles are both 45 degrees, and the two legs are equal in length. The length of the hypotenuse is √2 times the length of the legs. These triangles are helpful in Special Right Triangles 45-45-90 Tutorial Friendly Math 101 17.6K subscribers Subscribed Explore the key properties and theorems of 30°-60°-90° triangles. Learn how to solve and apply these special right triangles.

In the latest education blog post, learn more about the 45°-45°-90° Triangle, including its properties, strategies to solve and examples. Mathematics – Grade 9 Alternative Delivery Mode Quarter 3 – Module 13: Proving Conditions for Special Right Triangles First Edition, 2020 In a 45-45-90 triangle, each of the two acute angles is 45 degrees, making the triangle an isosceles right triangle. This means that the two legs (sides adjacent to the 45-degree angles)

Today’s first learning target is to notice and apply the relationship between the legs and hypotenuse of a 45˚,45˚, 90˚ triangle. The second learning target is to simplify radicals. While In today’s ratio of the lesson, we begin the transition from right triangle trig to the trigonometry with the unit circle. One of the main goals in this unit is a deep understanding of the unit circle. This will rely